Software Projects & Ancillary Material
- Component-based, functional dataflow architecture for auditing software & domainspecific functional programming language for stream-based data processing with applications in financial auditing (FSAE)
- Visual programming interface for data streams (VISFSAE)
- Game-theoretic decision procedure for CKn (cALC)
- Formal proof of confluence of λCKn in the theorem prover Abella
- Implementation of λCK in Haskell using Maps
- Lusterel Library - Combination of Lustre Data Flow and Esterel Control Flow
F# Analysis Engine (FSAE)
Author: Stephan Scheele
FSAE is a prototypical implementation of a component-based, functional dataflow architecture for a modern auditing software and exhibits the following features:
- Functional, domain specific language implemented in F#
- Component-based architecture
- Strongly typed data streams
- Parallel execution
- Encapsulation and compilation of auditing components
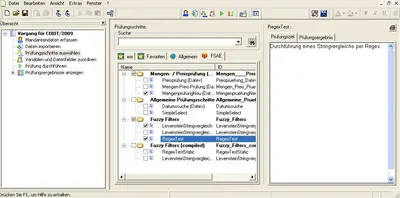
In the context of a feasibility study we integrated FSAE into DATEV Toolkit and demonstrated on the one hand how existing auditing script can be ported to FSAE and on the other hand implemented new functionality, e.g., a filters based on Regular Expressions or the Levenshtein string comparison.
Contact: Stephan Scheele
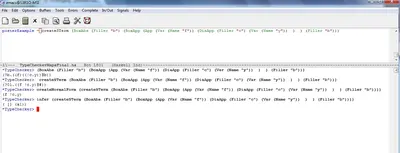
VISFSAE (Visual Programming System for FSAE)
Authors: Stephan Scheele, Thomas Kuhndörfer, Georg Zeissner
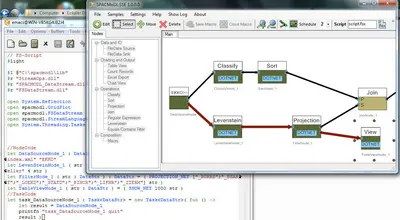
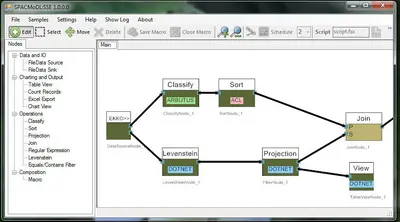
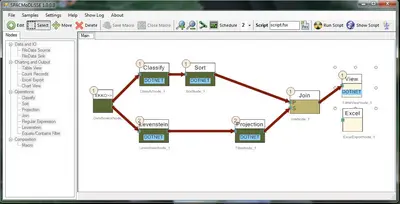
VISFSAE is a prototypical implementation of a visual programming environment which allows to modell an auditing proplem in terms of a directed dataflow graph. Nodes in the graph represent audit components which are particular, encapsulated algorithmic procedures which operate on streams of data tuples. An application programmer implements audit components, e.g., data extraction, data analysis, visulisation, etc. by composing existing operations. Such a dataflow graph is an abstraction of a real audit problem and can be compiled to a backend system, e.g. FSAE. Furthermore, the abstraction allows to transparently integrate different tools like data analysis software, algortithmic libraries, data mining libraries, reporting and charting tools under one common graphical user interface. Our prototype exhibits the following features:
- Interactive, visual programming of audit procedures
- Macro nodes
- Compilation to several backends, e.g., FSAE and ACL
- Parallel execution
Contact: Stephan Scheele
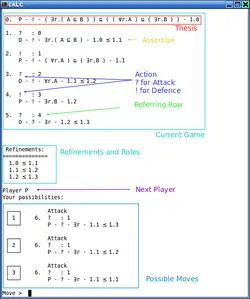
Game theoretic decision procedure for cALC
Author: Martin Sticht
In this work, a tableau based game theoretic decision procedure has been developed for the constructive Description Logic cALC which refines the classical semantics of ALC by a constructive interpretation. The decision procedure applies the ideas of dialogical logic introduced by Paul Lorenzen to cALC.
In this setting, the proof of a statement is the result of a game dialog between an opponent and a proponent. The two parties can attack or defend a given formula in a turn based fashion, where each move depends on a set of particle rules which restrict the ways to reason about a formula. Moreover, the flow the dialog is bound by so-called structural rules which handle the organisation of a game.
Each particle rule defines the way of how to attack or defend the argumentation of the other player, specified in terms of a cALC formula. They are said to state the local semantics whereas structural rules express the global semantics of a game dialog.
A prototype of the decision procedure has been implemented in Haskell in which two humans or one human against the computer can execute a game dialog in an interactive fashion.
Contact: Martin Sticht
Martin Sticht, Diploma Thesis: The Design and Implementation of a Game-Theoretic Decision Procedure for the Constructive Description Logic cALC
Formal proof of confluence of λCKn in the theorem prover Abella
Authors: Stephan Scheele, Alberto Momigliano
Tait/Martin-Loef style proof of Church-Rosser using parallel reduction.
This proof shows confluence for the (monomodal fragment of) lambda-CKn for closed terms. Commuting conversions are omitted.
It extends the work by Accattoli who gave an Abella proof of confluence for the simple lambda calculus. Here, we extend this by products, sums and contextual terms and associated reductions.
- Abella files(6.5 KB)
Mendler, M. & Scheele, S. (to appear), 'On the Computational Interpretation of CKn for Contextual Information Processing - Ancillary Material', Technical Report, Faculty of Information Systems and Applied Computer Sciences, The Otto-Friedrich-University of Bamberg, Germany
Accattoli, B. (2012) 'Proof Pearl: Abella Formalization of $\lambda$-Calculus Cube Property', in Ch. Hawblitzel and D. Miller, CPP 2012 , Lecture Notes in Computer Science, vol. 7679
Contact: Stephan Scheele
Implementation of λCK in Haskell through Maps
Authors: Johannes Gareis & Peter Kugelmann
This student project implements prototypically the simply typed λ calculus and its modally typed extension λCK in Haskell. It relies on a nameless representation of variables using so-called maps as introduced by Masahiko et. al where the position of each bound variable in a term is represented via a binary tree with each leaf having as value 1 for a bound variable position or 0 otherwise. The type inference mechanism based on Millners W-algorithm is extended for mapped λ-terms. The embedding into Haskell allows type checking and beta reduction of terms of the simply typed lambda calculus and its modally typed extension λCK.
Masahiko Sato, Randy Pollack, Helmut Schwichtenberg, and Takafumi Sakurai. Viewing λ-terms through maps.
Luis Damas and Robin Milner. Principal type-schemes for functional programs. In Proceedings of
the 9th ACM SIGPLAN-SIGACT symposium on Principles of programming languages, POPL ’82,
pages 207–212, New York, NY, USA, 1982. ACM.
Contact: Stephan Scheele
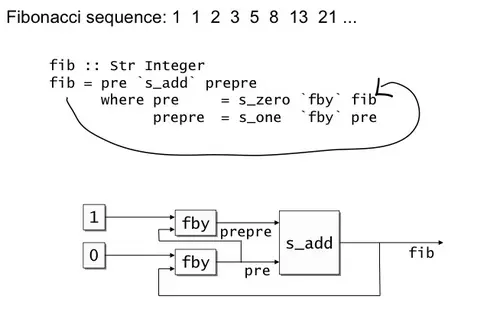
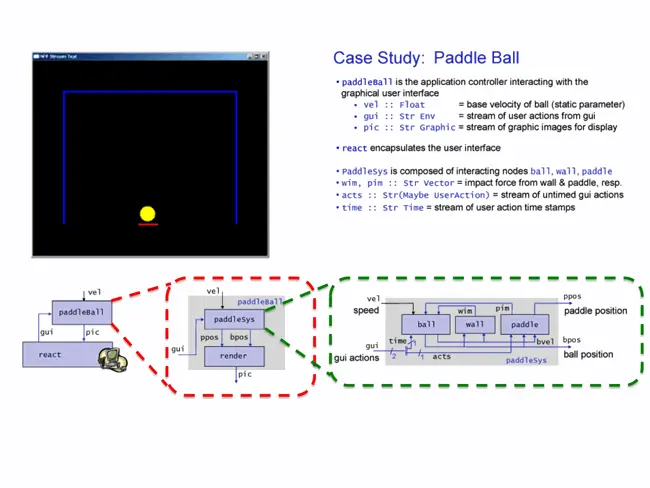
Lusterel - Integration of Lustre Data Flow with Esterel Control Flow
Authors: Michael Mendler, Joaquìn Aguado, Francisco Macias, Stephan Scheele
Lusterel is an experimental functional language currently built on top of the host language Haskell (a.k.a. lazy λ-calculus).
Lusterel consists of a simple set of well-understood functional combinators. So, it provides a uniform, smooth mapping between data and control flow and is extensible due to higher-order and polymorphism.
Many software systems such as for user interfaces, web services, business processes, games and hardware modelling, among others, are naturally composed of interactive processes. Where this is not the case, e.g. in graphics processing, it becomes increasingly important to decompose applications in order to leverage the processing performance available on modern multi-core execution architectures.
In these areas, an application is typically organised as a set of connected sequential processes, where executions can be abstracted in two ways:
- The data-flow view interprets inter-process communications as unbounded data streams changing over time and concentrates on functional relationships between streams.
- The control-flow abstraction perceives sets of connections at a particular time as interconnect states and analyses changes of such states.
In addition, processing is often organised into nested or interleaved computation cycles (phases) that can be associated with clocks running under the Synchrony Hypothesis. The synchronous paradigm for programming reactive systems gave rise to languages such as Lustre and Signal for data flow or Esterel for control flow. These languages, which have been very successful for embedded systems, so far have been developed mainly separately and around domain-specific tools (e.g., SCADE, Esterel Studio, SpecTRM, Simulink, Stateflow, Rhapsody) for use in control systems, automotive or avionics applications.
Yet, this state-of-the-art technology is not restricted to embedded system domains. The Lusterel Project aims to demonstrate that using a functional language like Haskell, it is possible to take advantage of the synchronous metaphors for a wider range of reactive applications. Lusterel is a Haskell library under development which provides a shallow embedding of Lustre and Esterel-style programming combinators. It coherently unifies both views for interactive applications without blurring the distinction between data and control. This contrasts with the traditional view which takes data flow as primary and flattens control in terms of explicit absence values introduced into the data streams. In this talk we show how standard Kahn-style data flow can coded in Haskell so that it can be scheduled, and thus smoothly combined, with synchronous control flow. Our co-inductive coding supports a variety of scheduling schemes, such as Esterel's 0-synchronous execution, bounded-buffer synchronisation and burst-mode multi-rate execution. Currently, the library only depends on the standard lazy lambda-calculus which provides sufficient operational structure to express single-threaded control flow. In the future we hope to extend this work to concurrent Haskell for multi-threaded execution.
More information is available on the Lusterel Library homepage.
J.Aguado, F.Macias, M.Mendler. The Lusterel Library: Programming Combined Data and Control Flow Applications in Haskell. ACM SIGPLAN 2009 Developer Tracks on Functional Programming (DEFUN 2009) in conjunction with The 14th ACM SIGPLAN International Conference on Functional Programming (ICFP 2009). Edinburgh, Scotland, September 2009.
J.Aguado and M.Mendler. Towards Strategies for Dataflow Programming. The 22nd Symposium on Implementation and Application of Functional Languages. (IFL 2010). Utrecht University in the Netherlands, September 2010.
J.Aguado, M.Mendler. Computing with Streams. Proceedings of the sixth workshop on Declarative Aspects of Multicore Programming (DAMP 2011), ACM Proceedings, ISBN 978-1-4503-0486-3, pp. 35-44, Austin, Texas, USA, January, 2011.
Contact: Michael Mendler