Interaction and Infection
Simulating the spread of a viral disease under non-pharmaceutical interventions from a social science perspective
Dominik Klein, Johannes Marx, Daniel Mayerhoffer & Jürgen Sirsch
Bamberg, 27 March 2020 (latest update: March 31)
Download pdf(1.0 MB)
The spreading of viruses in a population depends not only on biological factors and the availability of effective pharmaceutical products, but also on human behaviour. Since in the case of CoViD-19, there are currently no pharmaceutical measures available, the discussion focuses on non-pharmaceutical measures such as social distancing and quarantines. However, whether and to what extent these measures achieve the desired effects, does not only depend on medical parameters but also on human behaviour: A sufficient number of individuals need to change their social behaviour to successfully contain the spreading of CoViD-19. We offer an interactive computer simulation that allows us to compare different policy measures and social rules such as social distancing and quarantine in terms of their potential for virus containment. In the following text, we describe the basic structure as well as some implications of a simulation designed to model the effectiveness of different measures to contain the spreading of viruses like CoViD-19.
To run the simulation yourself, click here or on the picture below.
Disclaimer
This simulation is not intended to formulate concrete policy recommendations on its basis. For such an objective, the simulation would have to be more realistic and the characteristics of CoViD-19 would have to be calibrated more precisely in the simulation. Instead, it is intended to inform research to analyse and better understand social mechanisms of the dynamic spread of viral diseases. Furthermore, it can also be used for illustration, and as a tool for interactive understanding, in academic teaching and beyond.
Introduction: Why the containment of Covid-19 is also a social science problem
Infection with viruses and the treatment of resulting diseases are medical problems. What do social scientists have to contribute to these kinds of problems? The spreading of viruses depends not only on biological factors and the availability of effective pharmaceutical products but also on human behaviour. Since, in the case of CoViD-19, pharmaceutical interventions are not available at the moment, the focus of the debate right now is primarily on non-pharmaceutical measures. For these, it becomes clear that the containment of the CoViD-19 epidemic also has a social science dimension.
Thus, the effectiveness of political efforts to contain CoViD-19 mainly depends on whether the adopted non-pharmaceutical measures affect enough people and whether it really causes the affected individuals to change their behaviour: Do enough individuals adhere to political appeals to avoid close contact with other individuals? Does it help if the state recommends desirable behaviour, or should it sanction undesirable behaviour? What happens if only those who notice symptoms in themselves adhere to it? Furthermore, how does the spreading of the virus change if almost everyone sticks to the rules?
However, even if it would be possible to determine the sufficient level of participation in measures to reduce social contacts that would contain CoViD-19, we need to take into account the problem of collective action. Just because some behaviour is collectively rational does not imply that individuals would behave accordingly in order to achieve the necessary level of participation. The issue persists even if each individual in the population concerned would benefit from collective compliance. From an individual point of view, a collective-good problem arises: individuals cannot (or only with great difficulty) be excluded from the use of a collective good, even if they do not participate in the provision of the good. Possible containment measures of the CoViD-19 epidemic are an example of a collective-good problem. Often, it seems optimal from an individual point of view to let others adhere to the rules (and reaping the benefits of their compliance) while continuing to meet with people and not to restrict oneself. In such cases, coercive measures could be used to directly sanction non-compliance, thereby changing the incentive structure for individuals.
Furthermore, it is difficult to assess from an individual perspective how relevant the reduction of contacts is for the containment of the virus. The aggregated (combined) effects of the actions of single individuals are sometimes difficult to foresee. Here, the problem is to establish a connection between individual actions (contact avoidance vs non-contact avoidance) and collective effects (the spreading of the virus in the population). For example, is the social behaviour of single individuals sufficient to infect a whole population? Is putting only the infected persons into domestic quarantine sufficient for containing the epidemic, or should this measure also apply to persons with whom they had close contact? Or should measures be taken to restrict social contacts for all persons in the population? In order to adequately assess the effects of these measures, it is necessary to look at the dynamics that individual actions create on the collective macro-level. Frequently, complex patterns arise on the collective level out of the individual actions of a vast number of individual agents, which are not comprehensible for single individuals and are therefore not intended by them. In order to assess the collective effects of individual actions, it is therefore not enough to simply observe and explain individual behaviour. In addition, interaction patterns within social networks and complex societies require attention. Simulation models like the one provided here are suitable for assessing these complex aggregation effects. Simulations help us to understand how a gradual reduction of contacts can slow down the spread of the virus. And perhaps, they will also motivate the readers of this paper to do their part in creating the collective good, for the results of the simulation are clear: They show that the widespread compliance of individuals with the measures adopted by governments around the world is necessary to stop the spreading of CoViD-19 and avoid over-challenged healthcare systems which could save numerous lives.
At the same time, however, we must also issue a few warnings. The authors of this article are not medical professionals. The starting parameters used in the simulation are taken from current medical literature and publicly accessible online sources (see for example Ferguson et al. 2020, DOI: doi.org/10.25561/77482 and an der Heiden/Buchholz 2020, DOI: 10.25646/6571.2). Nonetheless, physicians are undoubtedly far better able than us to judge the extent to which these parameters are empirically correct. The platform we provide for simulating the dynamic spread of a viral disease can therefore be easily modified. You can change the parameters yourself via the input options of the model if you find the initial values we have set empirically implausible -- or if you wish to try out different what-if scenarios. Therefore, the model below does not intend to predict the actual spread of the coronavirus or to evaluate the efficiency of the various countermeasures accurately. Instead, it intends to illustrate central social mechanisms that underlie success or failure in the containment of CoViD-19 and to invite experimentation. In the best case, this model will help the reader gain a first impression of basic mechanisms of the dynamic spread of such viral diseases and to understand the mechanisms underlying possible countermeasures.
Model Description
Simulations can be understood as dynamic models of reality. They serve the purpose of capturing a section of the empirical world and identifying fundamental processes and mechanisms. For this purpose, simulation models have to make several assumptions. The following describes these assumptions for the present model. For the implementation of our simulation, we use the software NetLogo, which is freely available (see Wilensky, U. (1999). NetLogo. http://ccl.northwestern.edu/netlogo/. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.). Our model simulates the spreading of the virus in a population of 2000 people. This small population guarantees swift performance in a web environment; however, the results found here were robust in tests with larger population sizes. Expectably, the population density (i.e. the ratio of the number of persons to the size of the model world) influences the spreading of the epidemic.
Nevertheless, since the results of our simulation largely correspond to the empirically observed data (e.g. concerning mortality rate and spread dynamics of the epidemic), we assume that the chosen population density is appropriate for the purpose of our model. The individuals move in their immediate environment within the model world, which can be understood as their respective school, professional and private environment. Every encounter between an infectious and a not yet infected person results in the infection of the latter. Thus, an encounter of two individuals in the model does not represent every encounter in reality but represents every actual transmission of the virus (unless both individuals are already infected, or there are strict quarantine measures in place).
Government policies or individuals' voluntary actions, such as quarantine or restrictions on freedom of movement, which prevent the interaction of infected persons with non-infected persons (more on this below), are the only way to counteract an uncontrolled spread of CoViD-19 in the model. At each time step (tick), everyone moves once and also has the opportunity to infect others or become infected. For example, a time step can be understood as half a day, even though the nature of our model deliberately does not draw any direct parallel to reality.
After an infection, the colour of newly infected persons changes from blue to yellow, but nothing changes in their behaviour. After 8 tics (roughly corresponding to about four days), however, the person becomes contagious themselves, but without showing any symptoms. In the model world, the colour of the newly contagious person changes to orange. The user can set how long someone is infectious using the Timespan-Infectious parameter. According to currently available empirical information, this period seems to be short (in the model about 5-10 ticks).
After another 2 ticks, symptoms may break out, following current empirical estimates of CoViD-19, in two-thirds of the cases. People with milder symptoms are shown in red in the model, and after 10 ticks, their symptoms may worsen so that they have to go to the hospital. The probability of this to happen is by the parameter Likeliness-Hospital-if-Ill – here, a rate of 5-10% seems plausible. As people in the hospital do not move anymore, their shape changes from an arrow to a dot and their red gets slightly darker. After another 2 ticks, a third of the hospitalised need ventilation and 40% of those to be ventilated die 10 ticks later.
The model can simulate two approaches to contain the epidemic, namely social distancing and quarantine. Social distancing reduces the mobility of individuals (they no longer move around in the model world) and thus reduces the number of social contacts. However, in our model world, individuals practising social distancing can still come into contact with people, who do not distance themselves (for example, at work or while shopping). Therefore, infections will still occur. The model allows differentiating between three groups who can practice social distancing: Firstly, everyone who has symptoms (and are also interpreted by the affected persons as symptoms of CoViD-19 disease), set by ill-Distancing?. Secondly, a certain percentage of the patients’ social contacts, set by contact-Quarantine-Rate. Thirdly, a certain percentage of the total population as a precautionary measure, set by general-Distancing-Rate.
The second approach to contain the epidemic is called quarantine. Unlike social distancing, strict quarantine measures can never lead to infection. Our model always assumes strict quarantine for all persons in a hospital with CoViD-19. Optionally, quarantine measures can also apply to patients with milder symptoms (set the rate using ill-Quarantine-Rate in the model) and even their contacts (set the rate using contact-Quarantine-Rate in the model).
On the spread of the virus and the effectivity of possible countermeasures
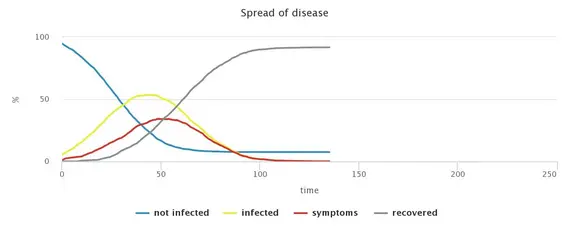
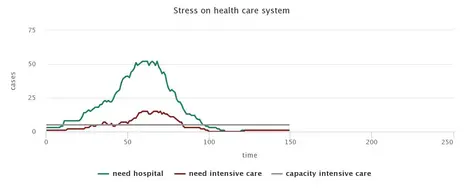
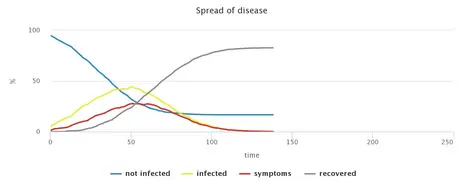
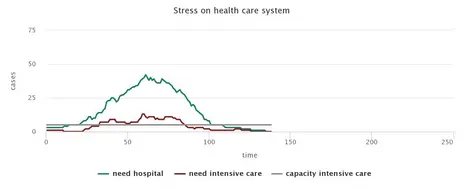
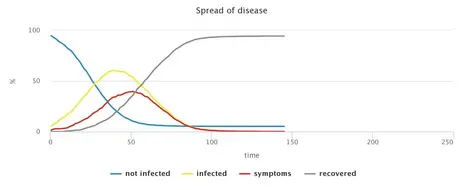
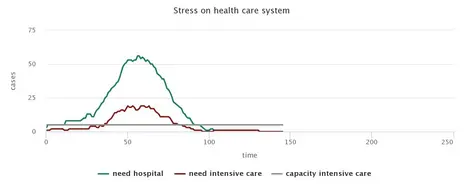
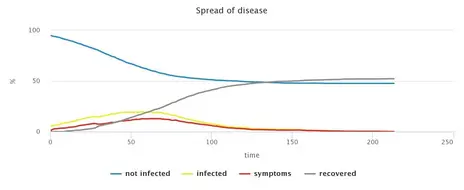
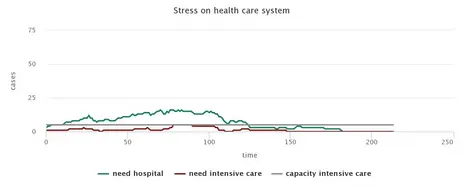
The simulation of a situation without any countermeasures shows the rapid spread of CoViD-19, which pushes the health system above its capacity limit. While the degree of infestation is reflected in the small proportion of remaining non-infected persons, the speed of the spreading of the virus can be read from the number of ticks until there are no more infectious persons.
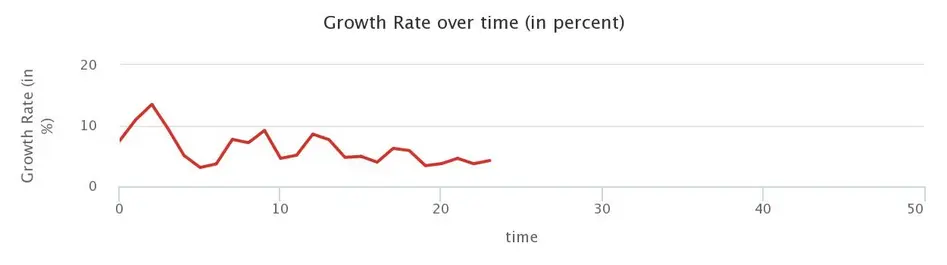
It is often reported in the media that the dynamic development of the CoViD-19 epidemic follows approximately an exponential function, i.e. the number of infected increases by a fixed percentage every day. The basic model version, without interventions to reduce contact frequency, shows this pattern in the growth rate, i.e. the rate of growth per time step (tick): the growth rate is relatively constant with a few small fluctuations. This observation holds up to an infestation of about half of the population. The fact that the further spread slows down with a higher degree of infestation is due to the herd immunity that is building up. This phenomenon can be observed comparatively early in our model due to its small population size. However, it is also generally observed in reality with propagation waves and can therefore also be expected for CoViD-19 if propagation progresses far enough.
There is a wide range of possible political measures to slow down and mitigate the wave of infection ("flattening of the curve"). We can only discuss a selection of possible measures here:
First, one policy measure is social distancing of the entire population. Even if only half of the individuals in the model comply with social distancing, this noticeably reduces the number of infected, and the speed of the virus spread. However, for these efforts to be sufficient for relieving the healthcare system, in our model, the compliance of 80% of the population would be necessary. To what extent such a high level of compliance is possible is difficult to assess: Firstly, individual motivation plays a role here; secondly, some moving individuals in the model represent people in system-relevant professions, where avoiding contact is impossible.
Alternatively, one could also formulate more specific measures and demand strict distancing only from those who show symptoms. However, this measure alone, without the participation of the general population, would only have a negligible influence on the occurrence of infections. After all, in the simulation, patients could still infect fellow humans who move around unrestrictedly despite distancing. (Here, there could be a relevant difference to the empirical situation: in reality, even one-sided distancing could prevent or at least limit the possibility of the virus being passed on). However, a combination of both measures would significantly increase their effectiveness. In order to achieve the same positive effects as in the case of 80% compliance, it would be sufficient if the symptomatically ill were to keep their distance from their fellow citizens consistently and if, in addition, 60% of the population were to participate in social distancing.
Finally, the model can also simulate the effects of our measure of strict quarantine if it were enforced not only in cases of severe disease progression with hospitalization but also on persons who only show mild symptoms. In contrast to simple distancing, quarantine reliably prevents infection because the patients no longer have any contact without comprehensive protective measures. In this scenario, the risk of infection is thus exclusively assumed to be posed by sick but (possibly still) symptom-free persons. However, these persons behave in the same way as in the scenario without intervention and can, therefore, continue to infect other persons.
Surprisingly, the model shows that such a quarantine measure is about as effective as social distancing with 80% compliance. However, one should consider that our model may underestimate the effect of social distancing, as, in our model, those who adhere to distancing can continue to be infected by those who move normally. In reality, it is expected that self-distancing leads to a lower general risk of being infected by others. Given the model parameters used here, however, strict quarantine could be sufficient to mitigate the wave of infection to such an extent that the health care system would not be overloaded. The stretching effect ("flattening of the curve") is even higher in the model than the one caused by social distancing, which can prove advantageous since the burden on the health care system can be relieved even better. However, this also implies an efficiency disadvantage since the time until the epidemic subsides is longer. Furthermore, the model assumes strict compliance of all people with symptoms. The prerequisite for the success of this measure is, therefore, not only that no one deliberately evades quarantine. Moreover, the symptomatic patients must know that they are suffering from Covid-19 and that their symptoms are not due to another disease and that they are in strict quarantine. Without the availability of a readily accessible test, all persons with relevant symptoms, whether they have Covid-19 or have other diseases, would have to be quarantined. As soon as the share of those with mild symptoms who comply with quarantine measures drops below 90%, the measure clearly loses effectiveness.
The graphs below summarise and illustrate the main simulation results:
No measures
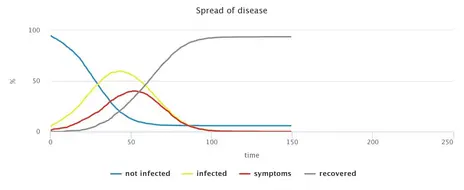
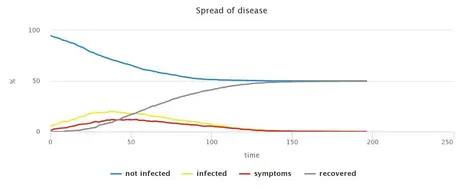
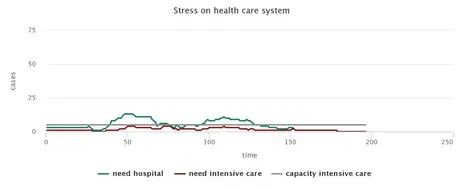
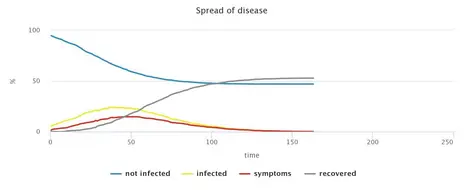
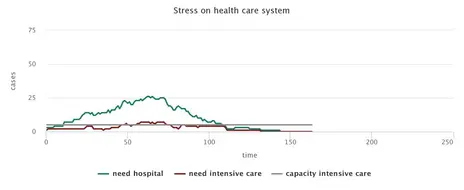
Alleviated restrictions, Smart Distancing and tracking of contacts
Increasingly, the debate focuses on whether to replace social distancing with alternative, less restrictive measures that are often called Smart Distancing. The present model allows to implement various such measures and analyse their possible consequences. In particular, variations of the model may combine a host of different policies, including general social distancing (applied to larger or smaller subgroups of the population) as well as targeted distancing or quarantining of sick people and possibly their contacts. Analysing such model variations is useful for assessing the robustness of the measures under different degrees of social compliance. In comparison with the most disruptive approach (general social distancing combined with strict quarantines of everybody infected), any relaxation of measures increases the epidemic’s spread. Naturally, which containment measures are judged sufficient will depend on what level of spread is considered acceptable, but also on the social, health or economic objectives pursued.
Consequently, the model permits the user to explore different packages of measures and their effects. We should note, however, that an exclusive focus on CoViD-19 patients and their immediate contact persons are only sufficient if these individuals exhibit very high levels of compliance. As discussed above, this may be difficult to achieve in reality. The model’s results, hence, suggest that such targeted measures should always be accompanied by broad approaches, e.g. social distancing among parts of the general population.
Tracing chains of infection has proven to play an essential role in combating the spread of CoVid-19, as this allows for quarantining contacts of infected persons or, at least, to apply adequate measures of social distancing. Contacts of sick persons can be identified by personalised analysis of mobile phone data, as is currently practised in China and partly also in South Korea. While this option is being discussed in various countries, its implications with respect to data privacy may be problematic. Just as in reality, it turns out to be advantageous to quarantine not only sick people, but also their contacts - or, at least, to encourage these contacts to restrict social interaction. However, in the model, identifying only some of the patients’ contacts is sufficient for effective containment. For this, no use of mobile phone data is necessary, as it suffices just to interview the sick. In fact, extending the measure to all contacts of sick patients does not add considerable value, at least in the model.
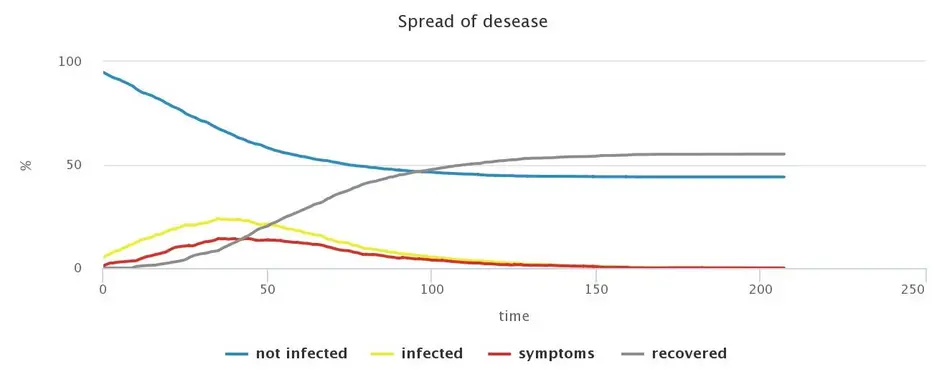
Set of measures consisting of general distancing (25% compliance), quarantine of patients (75% compliance) and quarantine of contacts of affected persons (25% compliance) and their distancing (75% compliance)
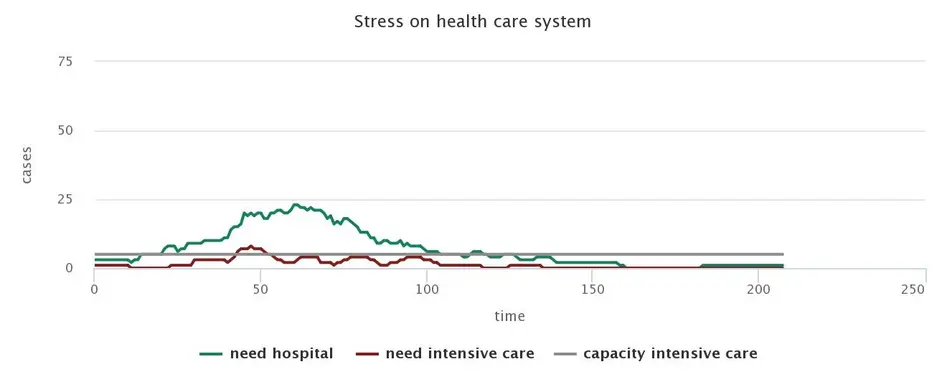
Different test regimes and their effects
Finally, we want to talk about another problem often discussed in the media. There are reports about significant national differences in the mortality of CoViD-19 patients, for example, when comparing China, Italy, Spain and Germany. Empirically, it is plausible that some differences exist, for example, due to the availability of intensive care, so that there may be actual differences in mortality between countries. In the simulation, however, these differences are not taken into account. Instead, we concentrate on the question of how national differences in the testing regime (i.e. how testing is carried out and who gets tested in a country) affect the reported mortality rates.
In general, the mortality rate is expressed as the proportion of the number of people who have died from a disease to the total number of people who have the disease:
The mortality rate (S) of a disease, here of CoViD-19, is defined as the number of patients who died from the disease (x) divided by the number of the population of sick people (y), i.e. SCoViD-19= x/y. However, time also plays a role here: The death rate should refer to the number of infected at the time when the fatally ill person was infected. The issue is neglectable if the growth rate of the epidemic becomes zero, and thus, the population remains stable. For our simulation, this means that the death rates depending on the different test regimes become comparable after the termination of the simulation run in question. The volatility of the curves (see below) is due to the exponential development of the numerator and denominator when they refer to different points in time and the growth rate between these points in time deviates significantly from zero.
In determining the mortality rate, differences can result, firstly, from the way the number of people who die from a disease is determined. For example, all casualties who have tested positive for the virus can count towards its death toll. In this case, the detection of the virus in the deceased would already be sufficient for them to be taken into account in the mortality rate, regardless of whether CoViD-19 was the actual cause of death. An alternative counting would include only those cases where the virus constituted the actual cause of death. For these individuals, infection with CoViC-19 would then be both a necessary and sufficient condition for dying. We will only focus on the latter case here.
In order to illustrate the influence of the test regime on the death rate, the simulation only considers those cases where the viral disease is the actual cause of death. However, this does not eliminate all problems. Uncertainty also exists in the estimation of the total number of infected individuals. Here, we face the problem of potentially overlooking large numbers of unrecorded cases. Thus, depending on the actual test regimes implemented, a greater or lesser number of cases will be unobserved.
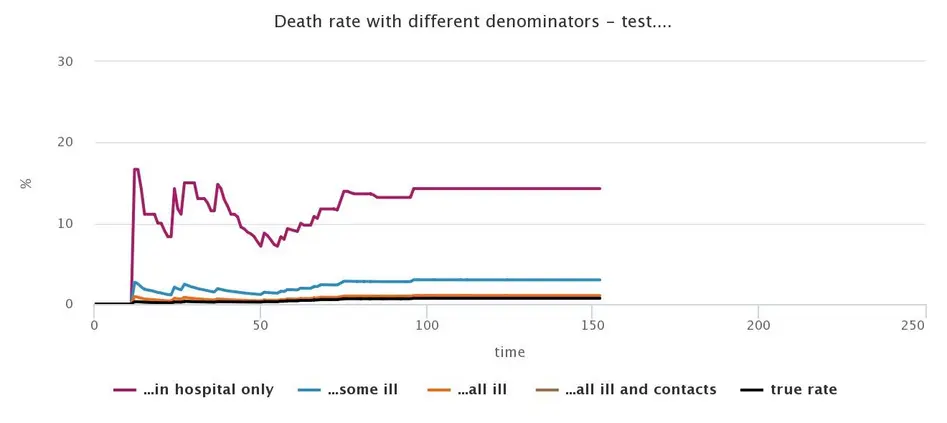
The following graph shows the influence of the different test regimes on the respective death rates for a standard run of our simulation without non-pharmaceutical interventions:
The chart presented here shows, for example, a mortality rate of just over 13% for the test regime in which the population of all infected is determined only by tests in hospitals. At the same time, if the initial variables and the course of the simulation were the same, a test regime that tests all symptomatically ill patients and their contacts would result in a mortality rate of less than 1%. This value corresponds almost exactly to the actual mortality rate in the simulation. However, this test regime produces errors when chains of infection arise from non-symptomatically ill patients who are traceable neither as patients nor contacts of a patient.
Finally, it should be remembered that we did not differentiate between age cohorts in the simulation. However, we know from empirical sources that the mortality of CoViD-19 is not constant across all age groups. However, we have ignored this factor in the simulation so that we can only model an average mortality rate here.
Overall, however, the simulation indicates that the testing of all patients and their contact persons could be a suitable method for estimating the actual number of ill people if it is not possible to conduct large scale (representative) tests of the whole population.
Outlook, conclusions and further works
Our simulation suggests that the catalogue of measures, as currently used around the world, could be a suitable instrument to contain the CoViD-19 epidemic. The simulation shows that high individual compliance with social distancing could slow down the dynamic spread of CoViD-19 to a level where the existing intensive care capacities would be sufficient. We come to this conclusion even though our model assumptions probably underestimate the effectiveness of social distancing as a measure: In our model, we assume (see explanation above) that individuals become infected every time they encounter an infected individual. However, behavioural changes not depicted in the model that are associated with social distancing (keeping distance, hygiene, etc.) plausibly reduce the probability of an infection when encountering an infected person.
A strict quarantine of all symptomatically ill persons also appears to be an effective measure in our model. In this case, however, it must be noted that all agents, even those with only mild symptoms, would have to adhere strictly to the quarantine. Hence, the required level of compliance on the part of the infected appears to be very high.
Alleviation of strict social distancing measures and a shift to smart distancing inevitably increases the spread of CoViD-19. Nonetheless, depending on the level of containment that one intends to reach (i.e., to reduce stress on the health care system), some sets of smart distancing measures prove sufficient in the model. For these measures, some of the contacts of individuals must be quarantined or asked to distance themselves, but reaching all or a high percentage of these contacts does not seem necessary. Hence, given the setting of our simulation, there seems to be no urgent need for a technical solution (like an app) to detect and notify the contacts of ill individuals.
In general, a key advantage of computer simulations is that they can be specified and adapted to new problems quickly and cost-effectively. These adaptations allow for a detailed examination of certain aspects or for an investigation of newly emerging issues which are in urgent need of evaluation. However, when interpreting the simulation results, it should be taken into account that simulations are based on assumptions and that these assumptions must be empirically adequate. This limitation applies, of course, to medical and epidemiological parameters, where social scientists can only rely on the current medical literature, but also to assumptions about the behaviour of individuals and their interaction. We have tried to make these assumptions in the text as transparent as possible in order to reveal possible weaknesses. Furthermore, simulations offer the possibility of modelling critical assumptions as variables in order to test the robustness of the results when the assumptions vary. We are convinced that this model is a good starting point to perform such work systematically, and to better understand mechanisms of the dynamic development of CoViD-19 and to formulate adequate policy measures.
Read more
If you are interested, the following literature reference will give you an insight into further application possibilities and limitations of simulations:
Klein, Dominik, Marx, Johannes, and Fischbach, Kai (2018): Agent-Based Modeling in Social Science, History, and Philosophy. HSR. Vol. 43:1. pp. 234-258. https://www.ssoar.info/ssoar/handle/document/56479
There are already isolated agent-based models that deal with the dynamic development of CoViD-19.
A well prepared and easily accessible simulation on this topic can be found on the website of the Bavarian Broadcasting Corporation: https://web.br.de/interaktiv/corona-simulation/
The Washington Post article on this topic and the simulation presented in it also offers a good introduction:
https://www.washingtonpost.com/graphics/2020/world/corona-simulator/